
Hello!
You have probably found this page because you have a "Sudokube" and want to solve it, or you just want to know what a "Sudokube" is.
The "Sudokube" or "Sudoku Cube" or "Sudoku Kube" is a Rubik's Cube that has numbered stickers on it instead of coloured stickers. The object of the puzzle is to arrange the cube in such a way that each cube face shows the digits 1 to 9 with no duplicate digits, similar to what you might see in a 3x3 block of the popular Sudoku puzzles. The digits do not necessarily have to be in order, depending on what kind of Sudokube you have.

Before you start trying to solve a Sudokube, you should familiarize yourself with how to solve a standard Rubik's Cube. I learned the Lars Petrus method, which is quite an easy method for beginners to learn. Once you have your Rubik's Cube skills down pat, you should understand the basics of how individual cubies move around and interact with each other. At this point you should be able to figure out the secrets of the Sudokube, but in case you are still having trouble, read on.
NEW: I was inspired to make a short video of me going through the solution of a cube that someone emailed me pictures of. The video only makes sense if you also read my explanation below.
The first thing you should realize is that once the cube is solved, all of the numbers on a given side will have the same orientation (except possibly for the one in the center -- we will get to that later). Using this information, you should be able to easily figure out where all the corners should be relative to each other.
The second thing you should realize is that the centers of each face are fixed relative to each other. This is the first thing you learn about basic Rubik's Cube solving.
Using these two pieces of information, you might be able to already figure out where all of the corners go relative to the centers. If you can, that's great! All we need to do is figure out where the 12 edge pieces go. If the corners are still ambiguous, we will have to do more analysis involving the edge pieces.

On my Sudokube, the eight corner pieces are labelled "771", "294", "595", "464", "629", "853", "113", and "687". You can see some of the corners and their orientations in the photos above and below. The six center pieces are "1", "7", "5", "4", "6", and another "1". Based on the orientation and the numbers I worked out that the only possible configuration of the cube is as follows:
1 2
6
7 9
3 71 24 69 1
1 7 5 4
8 46 59 85 6
4 5
1
7 3
(Sorry for the ASCII graphics... this is basically an "unfolded" cube with the centers and corners labelled.)
Note that this is all theoretical. There is no need to actually put the cube into this configuration, unless you want to visually convince yourself that it is correct.
OK, the edge pieces. For these guys we will use a combination of sticker orientation and Sudoku techniques to figure out where they go. First, let us label all of the different possible sticker orientations on the cube:
1 e 2
d 6 c
7 b 9
3 d 71 b 24 c 69 e 1
a 1 aa 7 aa 5 aa 4 a
8 g 46 f 59 h 85 b 6
4 f 5
g 1 h
7 b 3
On my cube there are eight possible orientation combinations for the edge pieces. I have labelled them "aa" to "hh".
I then made a list of all the edges that had matching orientations:
In my case, the final solution looked like this:
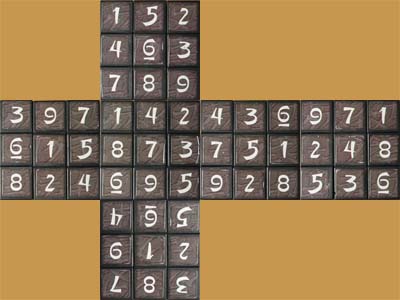
1 5 2
4 6 3
7 8 9
3 9 71 4 24 3 69 7 1
6 1 58 7 37 5 12 4 8
8 2 46 9 59 2 85 3 6
4 6 5
9 1 2
7 8 3
Once you have figured out where everything should go, you can use your standard Rubik's Cube skills to put it all into place. The only difficulty at this point is staying focussed and keeping track of what you have already solved, since it's not obvious at first glance!


There we go! I hope you found this useful!
Hosted by theorem.ca